Most dairy farms today collect data by which they attempt to make informed decisions about how to manage their herds. The problem is there are many types of data, and a good manager must understand the nature and limitations of the data being monitored to make informed decisions.

Reproductive data is particularly difficult to measure, which makes it a challenge to monitor, even on large dairy farms. Measuring reproductive performance is about measuring probabilities — the likelihood an event will occur. Unfortunately, the human brain is not very good at comprehending probabilities. Further, the nature of reproductive data involves a frustrating factor called randomness. The following points need to be considered and understood so good managers do not fall into incorrect conclusions about the reproductive data they collect on their farm.

What data is being monitored?

Data collected on dairy farms can generally be classified into two types. Continuous variables have an infinite number of possible values that fall between two extremes. Some examples of continuous variables measured on dairy farms are milk production, body weight, and feed intake. Measuring them requires a relatively small number of observations, and these variables tend to fluctuate by small degrees.

Categorical variables differ in nature. Most reproductive outcomes measured on dairy farms are a specialized subset of categorical variables called binomial variables, which have only two possible outcomes. Some examples of binomial reproductive outcomes include pregnancy outcomes (pregnant versus open), pregnancy loss (yes versus no), and calf sex (heifer versus bull). The challenge with binomial variables is that, by their nature, they are susceptible to randomness.

The law of large numbers

Jacob Bernoulli was a prominent mathematician whose most important contribution was in the field of probability, where he derived the first version of the law of large numbers. As an illustration of the law of large numbers, suppose 60% of the voters in Basel, Switzerland support the mayor. How many people must you poll for the chances to be 99.9% that you will find the mayor’s support to be between 58% and 62%? The answer that Bernoulli derived from his mathematics was 25,550 people — more than the entire population of Basel in Bernoulli’s day.

The problem is most dairy farmers succumb to the law of small numbers, which is the misconception that a small sample accurately reflects underlying probabilities. It is a misguided attempt to apply the law of large numbers when the numbers are not large.

Think of a coin flip in which the two possible outcomes are either heads or tails. The chances of getting a head or a tail are 50:50. The mathematical problem, however, is to determine how many times I must flip a coin to prove that the odds of getting a head or a tail are 50:50.

John Kerrich was a mathematician who performed a famous coin-flipping trial illustrated in Figure 1. A total of 10 or 100 flips did not approximate the expected outcome of 50% heads. It was not until he flipped his coin 1,000 times that the odds of getting a head approximated 50%.

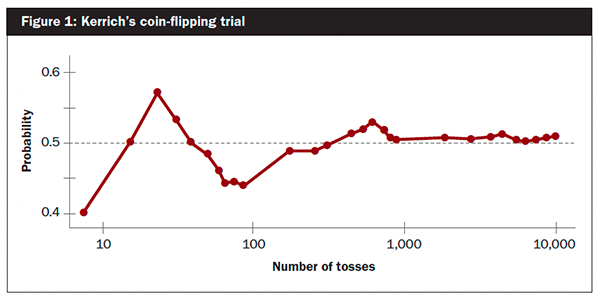
Think of each individual cow at a herd check as the outcome of a coin flip. Most farms check far fewer than 1,000 cows at a given herd check. The problem with measuring a binomial outcome such as a pregnancy diagnosis is, by nature, you need a lot of observations to approximate the actual conception rate in a herd. Further, if you base conception rate on too few observations, you introduce a lot of random noise in the outcomes, which creates variability that is difficult to distinguish from the actual value you are trying to measure.

“Good” versus “bad” herd checks

In this example, the “true” conception rate for these 200 cows is 30% (60 pregnant out of 200 total). The problem is pregnancy outcomes are subject to the law of large numbers, and most farms succumb to the law of small numbers.

For example, a farm may have only 40 cows to check at a given herd check. If the subset of 40 cows checked are represented in the figure by lines 2 and 3, the conception rate for that herd check is only 9 out of 40 or 23%. By contrast, if the subset of 40 cows checked are represented in the figure by the bottom two or top two lines, the conception rate for that herd check is 16 out of 40 or 40%. If a herd only checks 20 cows weekly, you can calculate the conception rate for yourself.

The law of small numbers introduces a lot of variability in the weekly herd check outcomes. In my experience, both veterinarians and farmers find this level of variation to be disconcerting to say the least. We now know this is the nature of measuring pregnancy outcomes which represent the variability typical for a binomial outcome. I can give many examples of farms that have struggled with what they perceive to be more than the expected number of bull calves born in a given period of time or the sporadic nature of twin births. All of these reproductive outcomes illustrate the randomness of reproduction that is inherent in measuring binomial outcomes.

We must understand variation

The best we can do with reproductive data is to understand its limitations and how we interpret the outcomes. It is human nature to look for patterns and to assign them meaning when we believe we find them. In each case, the longer the sequence, or the more sequences you look at, the greater the probability that you’ll find every pattern imaginable — purely by chance.

I encourage dairies to collect reproductive data but to understand the difficulties in measuring reproductive outcomes. Recognize that the outcome of weekly herd checks is going to be inherently variable. Do not panic if one herd check is worse than expected. A better approach is to monitor changes across time, such as with a mathematical weighted average that can “smooth out” the weekly variation in pregnancy outcomes.

Finally, larger dairy farms with more data have less weekly variability than smaller farms with fewer cows. While unfortunate, that is the nature of reproductive outcomes. Still, even the largest farms will have some degree of variability in reproductive outcomes due to the law of large numbers. In the end, the randomness of reproduction is something we all must learn to deal with and understand when interpreting reproductive data on dairy farms.